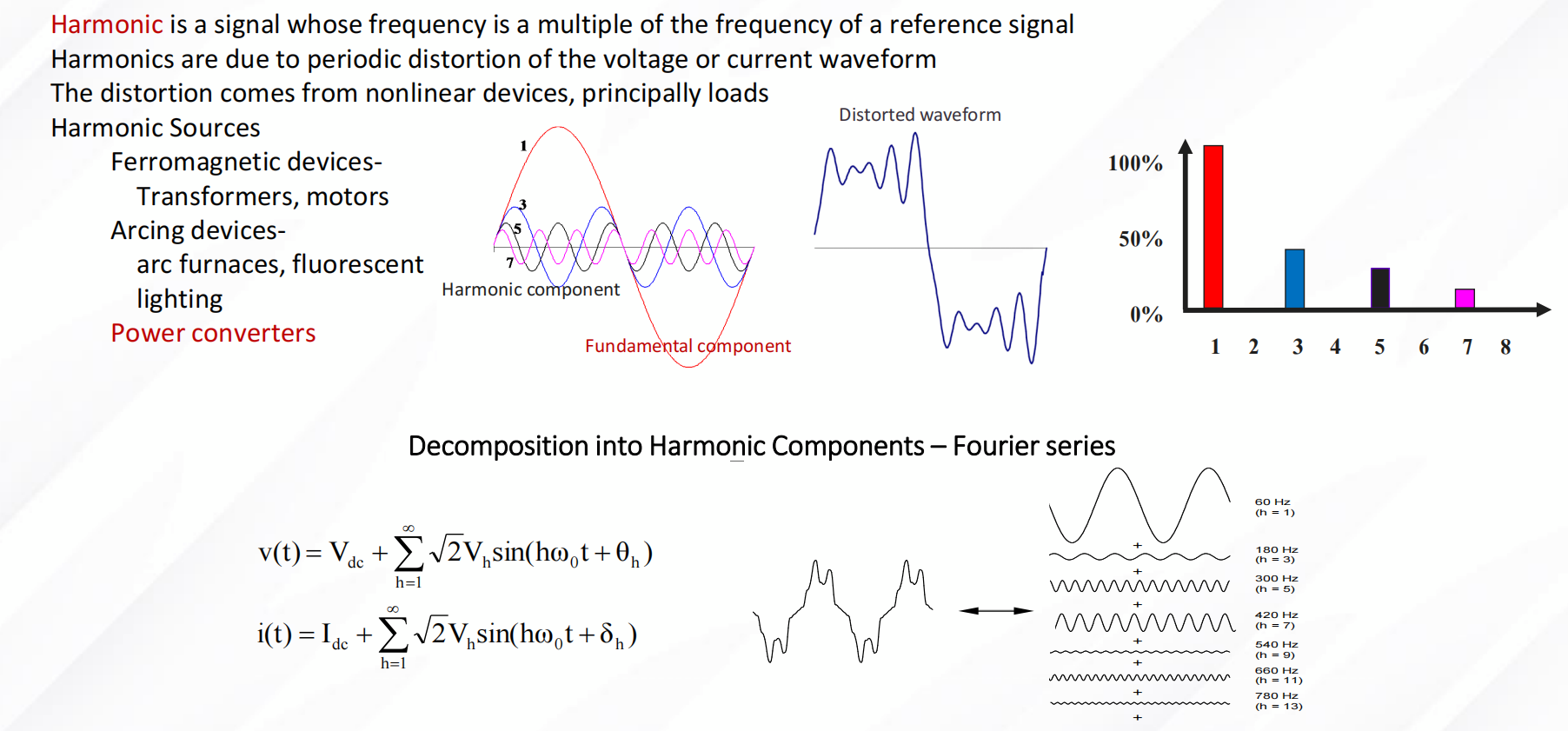
The peak and effective value of harmonics

The peak and effective value of harmonics

When discussing the peak of harmonic currents, it's essential to first understand the fundamentals of harmonics. The effective value (RMS value) of a harmonic describes the average power of the harmonic component over one period, reflecting the equivalent extent to which the harmonic causes heating effects in the system. However, the peak of a harmonic (the instantaneous maximum value) is determined by its amplitude, which corresponds to the highest point of a complete sinusoidal waveform.

In the context of power systems and other signal processing areas, if the effective values of harmonics are the same, as the harmonic order (frequency) increases, based on the properties of the sine wave, its peak indeed becomes higher. This is because for sine waves with higher frequencies, the same amount of energy is distributed over a shorter time interval, implying a faster rate of change per unit time, thereby resulting in larger instantaneous peak values.

For example, suppose the fundamental wave and a high-order harmonic both have an RMS value of Vrms. Then:

Vpeak = √2 * Vrms.

For harmonics, if we assume there are n harmonics with identical effective values of Vrms, and the m-th harmonic has a frequency that is m times that of the fundamental frequency, then the peak amplitude of the m-th harmonic can also be calculated using the above formula:

Vpeak_m = √2 * Vrms_m.

Now, even if the total harmonic current's effective value is constant, the peak of an individual harmonic does not increase solely due to a rise in frequency. Yet, in the case of the total harmonic current, because of the rapid-changing nature of high-frequency harmonics, these may reach their individual peak levels multiple times within a short duration, which increases the likelihood of the overall total harmonic current having a larger instantaneous peak than when only lower-order harmonics are present.

Assuming the total harmonic current is the sum of all harmonic components:

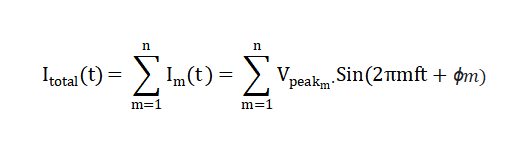
In this superposition process, while each harmonic maintains a fixed effective value, high-order harmonics, due to their faster rate of change, could simultaneously reach their peak levels at a specific instant, thereby causing the instantaneous peak of the total harmonic current to be higher than when only low-order harmonics are considered.

It's important to note that the above discussion is based on an idealized model. In real-world power systems, harmonic issues must also take into account factors such as nonlinear device characteristics and filter performance, which might influence the actual harmonic current peak levels.